对时间的处理，是分布式系统协议设计的一个关键问题。因此，我准备花一些精力，将这块的知识简单整理一下，尽可能简单的系统化呈现出来，作为自己学习的一个知识点梳理¹。

分布式系统和传统的单机系统不同，彼此是通过网络而不是”主板”连接、消息通讯是不可靠的。因此如果没有任何同步机制，同一系统的成员之间无法确保时间戳的误差控制在某个范围内。这个基本条件的缺失，会给上层应用的设计带来很多的麻烦。比如，一个业务流程的两个阶段分别在两台机器上处理，而后在第三台机器上将处理记录join起来，就可能因为时间戳的问题引发混乱。如何做好时间同步的协议，成为了分布式系统中的一个基本的问题。

在系统对时的时候，有两类基本的协议，第一个是外部对时，简单的说，就是整个分布式系统中的所有成员，与外部某个指定的源头进行时间同步，确保与源头的时间的diff在某个误差范围\(D\)内; 另一种是内部对时，即内部通过广播等各种手段，确保系统内的成员俩俩间的时间误差在一定范围内。从这里可以看出，如果一个集群使用了外部对时，控制误差在\(D\)以内，那么这个集群内部的时间的误差，也一定能够控制在\(2D\)的范围内。但反过来不一定，因为有可能整个集群与外部的时间存在很大的整体偏差，尽管在内部彼此的偏差很小。

那么如何进行时间的同步呢？这里介绍两个经典的协议：Cristian和NTP。

Cristian的基本过程是这样的，假定现在P进程要从授时服务器S获取时间，那么最朴素的做法就是P向S发送请求，S将自己的时间t返回给P，而后P设置自己的时间为t。这个做法存在一个很关键的问题，就是由于网络的通讯时间是不确定的，P拿到t的时候，已经经过了不确定多久了，无法估计结束后P与S的时间误差范围。因此，我们需要将网络通讯的时间，即RTT(Rount Trip Time)也考虑进来。在这个场景下，RTT指的是P进程发出请求，到得到S的回应消息的时间差，这个时间差是P进程自己可以记录求得的。假定我们知道从\(P \to S\)的最小延时是\(min_1\)，\(S \to P\)的最小延时是\(min_2\)，那么，我们可以推断，真实的时间在\([t+min_2, t+RTT-min_1]\)区间内，Cristian的做法就将对时结果设置为：\(t'=t+\frac{RTT+min_2-min_1}{2}\)这个中间位置上。那么，其误差就能控制在\(\pm \frac{RTT-min_1-min_2}{2}\)的范围内。

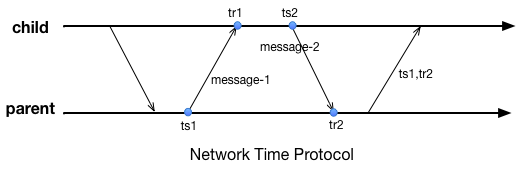
另外一个知名的时间同步协议是NTP，全称Network Time Protocol。NTP协议一般在某个大的机构内部署，将机构内的设备组织成树形结构，每个节点都从父节点处获取时间。整个同步过程分为两轮，第一轮父节点记录自己发送返回的时间点\(ts_{1}\)，子节点记录自己接收到返回消息的时间\(tr_{1}\); 而后第二轮，子节点记录自己的发送时间\(ts_{2}\)；父节点记录收到请求的时间\(tr_{2}\)后将\(ts_{1}\)和\(tr_{2}\)返回。那么子节点可以计算出自己和父节点之间的时间偏差为: \(o=\frac{(tr_{1}-tr_{2}+ts_{2}-ts{1})}{2}\)，并以此为依据进行修正(一般需要确保时间不能“倒流”)。那么为什么\(o\)是这么计算呢？假定子节点与父节点的时间偏差(offset)为\(o'\)、父节点往子节点的通讯时延为\(L_{1}\)、子节点往父节点的通讯时延为\(L_{2}\)，那么:

相减可以得到:

因此:

由此可知o的这个值也在RTT相关的一个误差范围内，是可估计的。

从上面两个协议可以看出，对时的误差是与RTT强相关的。由于消息的传递受制于光速、距离越远时间准确度的保证就越差。对于那些假定了时间误差在某个范围内的分布式协议，在跨越距离很大的时候，我们就必须要将这个误差对系统的影响考虑在内，这将显著增加分布式系统设计的复杂度、或者影响设计出来的系统的吞吐(尤其是有高一致性要求的事务型系统)。

最后，不论是Cristian还是NTP，都只描述了一次对时如何将时间的偏移(clow skew)控制在一定范围内。由于不同机器的时钟的行进速度(clock drift)是不同的，因此我们需要每隔一段时间，进行一次修正，以消除时钟节奏不同的影响。多久需要做一次同步呢? 这个做一个简单的计算就可以得到。假定系统整体时钟的行进速率与标准时钟的速率小于MDR(Max Drift Rate, 一般由时钟的实现方式决定)，那么系统内俩俩时钟的行进速率差小于2MDR。如果我们要求系统内时间差不能超过M，那就必须以不低于\(\delta = \frac{M}{2 \times {MDR}}\) 的间隔进行时间同步。在现实的系统中，我们需要计算合理的M，以避免系统内出现过多的时间同步消息。