在人工智能发展的早期阶段，科学家们的大思路是通过构建完备的逻辑演化系统，将各种规则输入计算机后由计算机进行模拟计算。但现实世界是相当复杂的，基于规则演化模型的人工智能效果并不理想。因此，有人提出了仿生学的思路，即模仿人的大脑结构、仿真神经元组建而成的神经网络的工作过程，来实现人工智能的终极目标。

那么，这个思路是否可行呢？显然可以，因为人脑就是这么运作的！真正需要解决的问题是如何用计算机建模出人脑的工作过程，以及仿真人脑需要巨大的、高度并发的算力，外加用于机器观察学习所需的大量的数据。在计算机硬件以及大规模分布式系统的成型、互联网的普及后积累了大量的可用于训练的数据的今天，训练实用神经网络的所需的条件逐步成熟，因此催生了当下繁荣的深度学习应用。

这篇文章是deeplearning.ai系列的第一门课的归纳总结，主要介绍了一些深度学习的基本概念，是后续所有课程的基础。

神经网络的构成

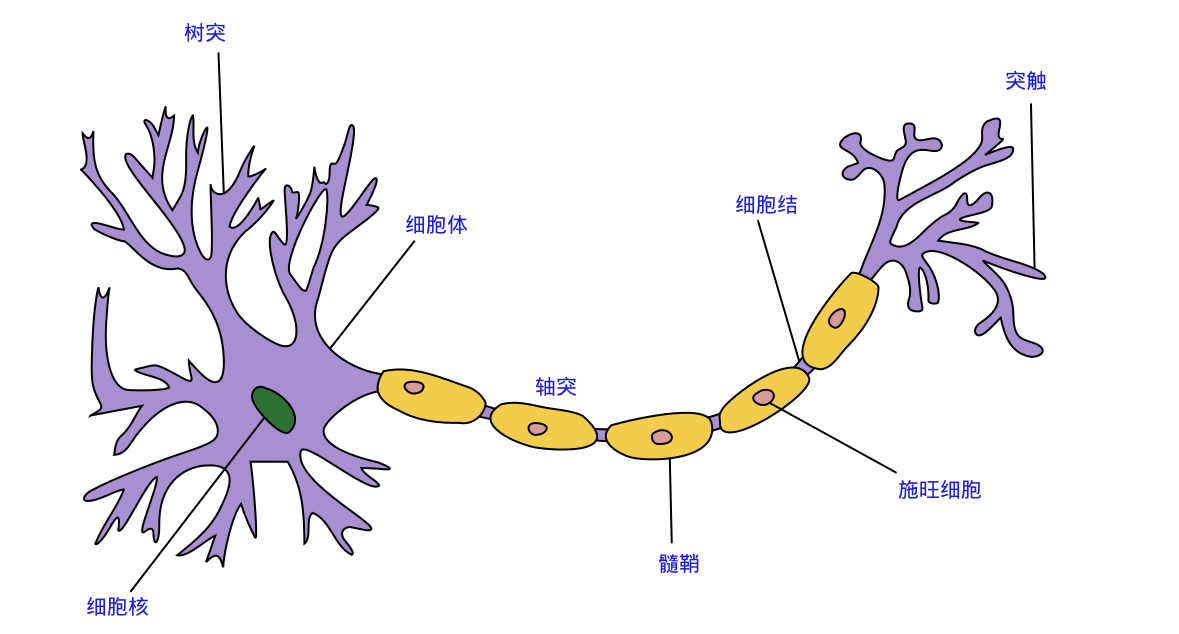
一个典型的神经网络(Nerual Network)是由基础的”神经元”(Neuron)构成。在真实的人脑中，神经元由树突接收来自其他神经元的信号，汇聚所有树突收集的信号、并经过一定处理后，产生一个新的信号发送到下游其他神经元。计算机中的Neuron的结构非常类似，它接收来自上游的k个信号\(x_k\)，而后经汇聚(一般采用\(z=\sum_{i=0...(k-1)}{(w_i * x_i + b_i)}\)的方式)、经激函数(activation function, 一般记为\(\sigma()\)处理后(\(a=\sigma(z)\))，将结果\(a\)发送到下一组神经元中。在每一个神经元中，有一些重要的要素，首先是公式中的\(w_i\)和\(b_i\)，这些被称为参数(parameter)，这些参数是后续需要通过训练算法需要计算出数值来的；另外一个\(\sigma\)，也就是激函数(activate function)，激函数对汇聚后的信号执行一个非线性的变化后得到单个神经元的输出结果。常见的激函数包括: sigmoid、tanh和ReLU等。

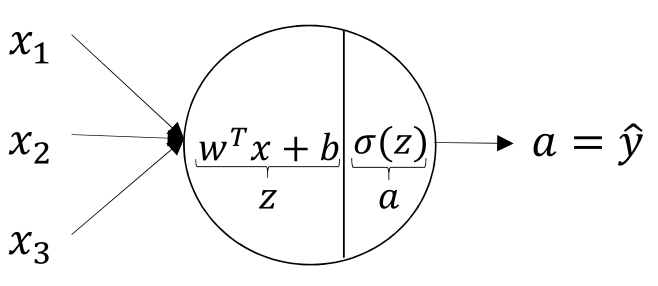
接着，众多神经元组建成神经网络。基本形态如下图所示

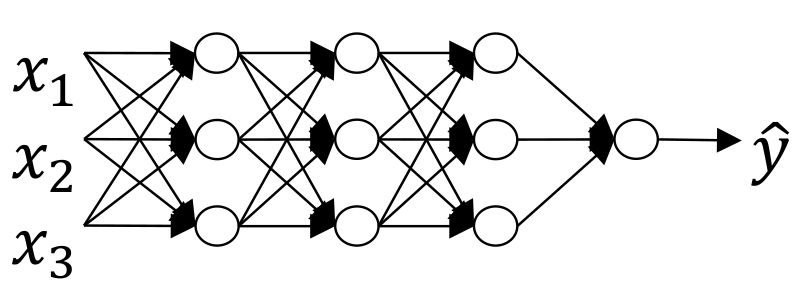
每当我们输入一个\(\vec{x} = \left( \begin{array}{ccc} x_1 \\ x_2 \\ \vdots \end{array} \right)\)，经过逐层计算，就能够得到最终的输出结果\(\hat{\vec{y}} = \left( \begin{array}{ccc} y_1 \\ y_2 \\ \vdots \end{array} \right)\)。

模型训练的基本过程

从前一节的描述中我们可以知道，神经网络这样的一个”大脑”，是由\(w\)和\(b\)这样的”参数”和神经元之间的拓扑关系构成，我们也把这个参数+拓扑，称之为一个模型(model)。在应用场景中，我们一般将通过样本数据得到模型的过程称之为训练(training)，而将基于某个训练好的模型、在某个输入下的计算过程称之为推理(inference)。推理的计算过程非常好说，就是按照前面的公式，基于已经算好的所有参数，带入计算即可；而训练，目前大部分采用的是基于反向传播算法(backward-propagation)进行的。

训练模型大概可以分为如下几步：

• 前向传播(Forward-Propagation)：即输入训练数据样本，经过神经网络的逐层计算，得到对应的一组输出；
• 比较输出结果与样本中的”正确值”，计算cost function的数值。一般而言，偏差越远cost-function数值越大；
• 反向传播(Backward-Propation)：将cost function中的差值，采用诸如”梯度下降法”(Gradient-descent)的方式，逐步”分解”到前一层网络中，修正每一层中的\(w\), \(b\)的数值；
• 对训练集执行了前三个步骤，被称为一个epoch。每执行完一个epoch，基于当前训练得到的\(w\)与\(b\)的参数值，送入dev样本集计算此时的cost-function。如果cost足够小、达到了收敛条件，则训练结束、输出对应的\(w\)和\(b\)；否则继续执行下一轮epoch，迭代出更好的\(w\)与\(b\)的取值。

整个训练过程本质上是一个最优化过程，即通过一系列手段，得到使得定义的cost function值最小的参数的集合。

在实际应用中，我们可以将上述训练过程，用矢量化的形式表达出来。这样一来，整个计算过程就可以看作是一系列矩阵和矢量的运算，并通过调用经过充分优化的数值计算库，充分发挥硬件性能，缩短训练时间。

Logistic Regression

为了说明问题，我们可以先以最简单的、仅有一层神经网络的LR算法为例，呈现整个计算过程。

LR是一个非常有名的算法，在DNN开始风靡之前，LR在计算广告学以及许多领域，都存在广泛的应用。LR所解决的被称为二元分类问题，即给定一组“特征”，输出0或者1作为结果。比如在线广告的CTR预估，通过提取广告和用户侧的各种特征信号，经过某个模型以后，估计用户可能(output=1)或者不可能(output=0)点击这条广告，从而基于这个判断选择最可能被用户点击的广告进行展示¹。

LR神经网络的基本形态如下图：

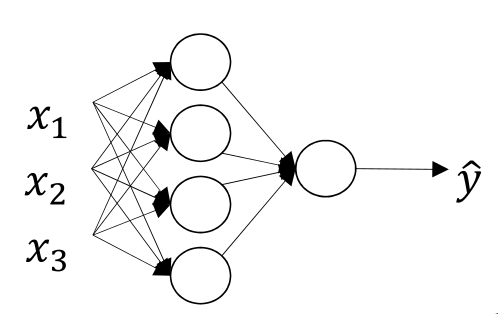
以CTR预估为例，假设我们需要预测一个用户是否会点击某条广告，需要考虑三个方面的基本信息：标题与搜索词的重合度(\(x_1\))、用户的id(\(x_2\))、广告主id(\(x_3\))。通过一系列的调研，研究者采集到了\(m\)个\(\vec{x}=\left( \begin{array}{ccc} x_1 \\ x_2 \\ x_3 \end{array} \right) \to y(ctr)\)的样本数据，现在希望构造一个函数\(f\)，期望后面可以直接通过计算\(y=f(\vec{x})\)函数，估算出给定\(x\)后的ctr预估结果。

LR假定函数\(f\)的形式为:

其中， \(\vec{x}=\left( \begin{array}{ccc} x_0=1 \\ x_1 \\ x_2 \\ \vdots \\ x_k \end{array} \right)\), \(z=\sum_{i=0 \dots k}{w_i \cdot x_i} = \vec{w}^{T} \cdot \vec{x}\)，在这个式子中，我们可以看出\(f\)的结果必然是一个介于\([0, 1]\)的实数。

假若我们每次送入一个样本，那么我们可以得到: \(\hat{y}^{(i)} = f(\vec{x}^{(i)})\)。我们期望\(\hat{y}^{(i)} \approx y^{(i)}\)。为衡量与预期之差异的大小，定义针对单个样本的Loss Function为:

在这个Loss function的定义中：

• 如果\(y^{(i)} = 1, 则\mathcal{L}(\hat{y}^{(i)}, y^{(i)}) = \log(\hat{y}^{(i)})\)，\(\hat{y}^{(i)}\)越接近1(\(=y^{(i)}\))，\(\mathcal{L}\)越小。
• 如果\(y^{(i)} = 0, 则\mathcal{L}(\hat{y}^{(i)}, y^{(i)}) = (1 - \hat{y}^{(i)}) \cdot \log(1 - \hat{y}^{(i)})\)，\(\hat{y}^{(i)}\)越接近0(\(=y^{(i)}\))，\(\mathcal{L}\)越小。

每当我们完成一个epoch, 我们可以将所有样本的\(\mathcal{L}\)综合起来，得到总的Cost Function:

至此我们完成一轮的计算。所谓的机器学习训练，在这里，就是通过各种各种最优化算法，求解使得\(\mathcal{J}\)最小的那组\(w\)的集合。最优化的手段其实很多，比如大家最容易理解的梯度下降法：

这个式子很好理解，即调整参数\(w\)，让其朝着\(\mathcal{J}(w)\)变小的方向”迈进”\(\alpha\)长度，一般而言\(\mathcal{L}(w') \le \mathcal{L}(w)\)。反复迭代若干个epoch后，我们可以找到使得\(\mathcal{L}\)最小的那组\(w\)的值，也就是得到我们的训练结果。

LR训练过程的矢量化表达

为提高计算效率，我们可以将整个训练过程矢量化。具体做法为，假设我们将第\(i\)个样本的输入记为\(\vec{x}^{(i)} = \left( \begin{array}{ccc} x^{(i)}_0 = 1 \\ x^{(i)}_1 \\ x^{(i)}_2 \\ x^{(i)}_3 \end{array} \right)\)，而将所有\(m\)个样本堆叠而成的矩阵记为

$$\begin{aligned} X &= (\vec{x}^{(1)}, \vec{x}^{(2)}, ... \vec{x}^{(m)}) \\ &= \left( \begin{array}{ccc} x^{(1)}_0 & x^{(2)}_0 & \cdots & x^{(m)}_0 \\x^{(1)}_1 & x^{(2)}_1 & \cdots & x^{(m)}_1 \\ x^{(1)}_2 & x^{(2)}_2 & \cdots & x^{(m)}_2 \\ x^{(1)}_3 & x^{(2)}_3 & \cdots & x^{(m)}_3 \end{array} \right)_{4 \times m} \end{aligned}$$ $$Y=(y^{(1)}, y^{(2)}, \cdots y^{(m)})_{1 \times m}$$

那么可以表达为:

$$\begin{aligned} \vec{z} &= w^T \cdot X \\ &= \left( w_0, w_1, w_2, w_3 \right)_{1 \times 4} \cdot \left( \begin{array}{ccc} x^{(1)}_0 & x^{(2)}_0 & \cdots & x^{(m)}_0 \\x^{(1)}_1 & x^{(2)}_1 & \cdots & x^{(m)}_1 \\ x^{(1)}_2 & x^{(2)}_2 & \cdots & x^{(m)}_2 \\ x^{(1)}_3 & x^{(2)}_3 & \cdots & x^{(m)}_3 \end{array} \right)_{4 \times m} \\ &= \left( w^T \cdot x^{(0)}, w^T \cdot x^{(1)}, \cdots, w^T \cdot x^{(m)} \right)_{1 \times m} \end{aligned}$$

而后基于这个计算方式，执行element-wise的计算，得到对应的\(f\)和\(\mathcal{L}\)、\(\mathcal{J}\)等值。

深层神经网络(DNN)

当我们把LR中的神经元的层次增加到足够多的时候，我们就得到了深层神经网络(Deep Nerual Network)，而通过类似前述的训练方法得到Parameter集合的过程，就被称为深度学习(Deep Learning)。

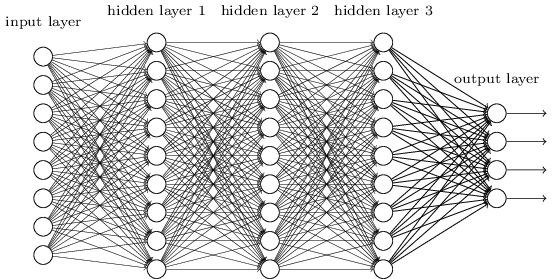
假设我们存在\(L\)层网络，其中第\(l\)层有\(n_l\)个神经元。那么，整个网络就共有\(\sum_{l=1}^{L}{(n_{l-1} \times n_l + n_l)}\)个参数²。这些参数使得DNN可以表征出纬度更高、特征更多的模型。现实中也确实如此。这几年的研究表明，在计算机视觉、语音、自然语言理解方面，DNN都表现出相当不错的效果。但同时，由于参数规模和计算量的上升，有导致了众多工程问题的出现，从而出现了诸如TensorFlow、pyTorch这类的软件框架，以及GPU/TPU的计算硬件的应用，此为后话。