前面介绍了深度学习训练中使用的最基本的梯度下降法，在实际应用中，往往需要在基本的梯度下降法中做一些调整，以加速收敛、减少模型训练的时间。

首先，是样本数据规模的问题。基本的梯度下降法，采取的是每次都是对所有的样本数据执行前向传播后，再计算cost及进行反向传播。在现实的场景中，Training集合的样本数量非常巨大，因此需要经过巨大的计算后，才进行一次梯度的更新，比较低效。一种朴素的想法就是我将集合分成若干个小数据集(mini-batch)，然后每做一批就进行一次反向传播、更新所有的参数，这种算法被称为mini-bach gradient descent。这样一来，每次反向传播需要计算的样本数据规模就是可控的，所需的计算量也显著减少了。需要特别注意的是，如果我们每批次送入的数据，小到只有一条，就变成了一种被称为SGD(Stochastic gradient descent)的优化方法，这个优化方法经常会在文献中见到。

另外一个常见的改进方式是引入”Momentum”。什么意思呢？如果我们把梯度下降法的优化”路径”画出来，会发现经常会出现如上图中的”抖动”现象。我们想减少抖动，让梯度方向更加聚焦一些。具体做法非常简单，就是在计算下一个梯度方向的时候，参考历史的梯度信息，并基于此做一些修正。比如，当前这轮计算的梯度结果为\(dW_i\)，前一轮计算结果为\(dW_{i-1}\)，那么我们在计算的时候，可以采用修正后的\(dW_{i}' = dW_{i} + \beta \cdot dW_{i-1}\)作为梯度方向来进行调整。这种调整其实本质上是对历史数据做了某种程度(由\(\beta\)的大小控制)的”加权平均”。当然，前面的式子是最简单的。现实中，更多的采用被称为RMSprop或者Adam-optimization的方法进行这个梯度方向的修正，效果会更好。

最后一个需要介绍的是对梯度下降法的步长(learning rate)进行修正。一般直观的认为，梯度下降法在早期、离最优解的距离比较远，因此可以采用较大的步长快速接近目标；但当接近最优点的时候，则需要缩小步长，避免一不小心跨过了最优点，在最优点的周边盘旋。因此，经常采用一些类似\(\alpha_i = 0.95^{t} \alpha_{i-1}\)、\(\alpha_i = \frac{k}{\sqrt{t}} \alpha_{i-1}\)之类的式子，逐步减少步长(learning rate decay)。

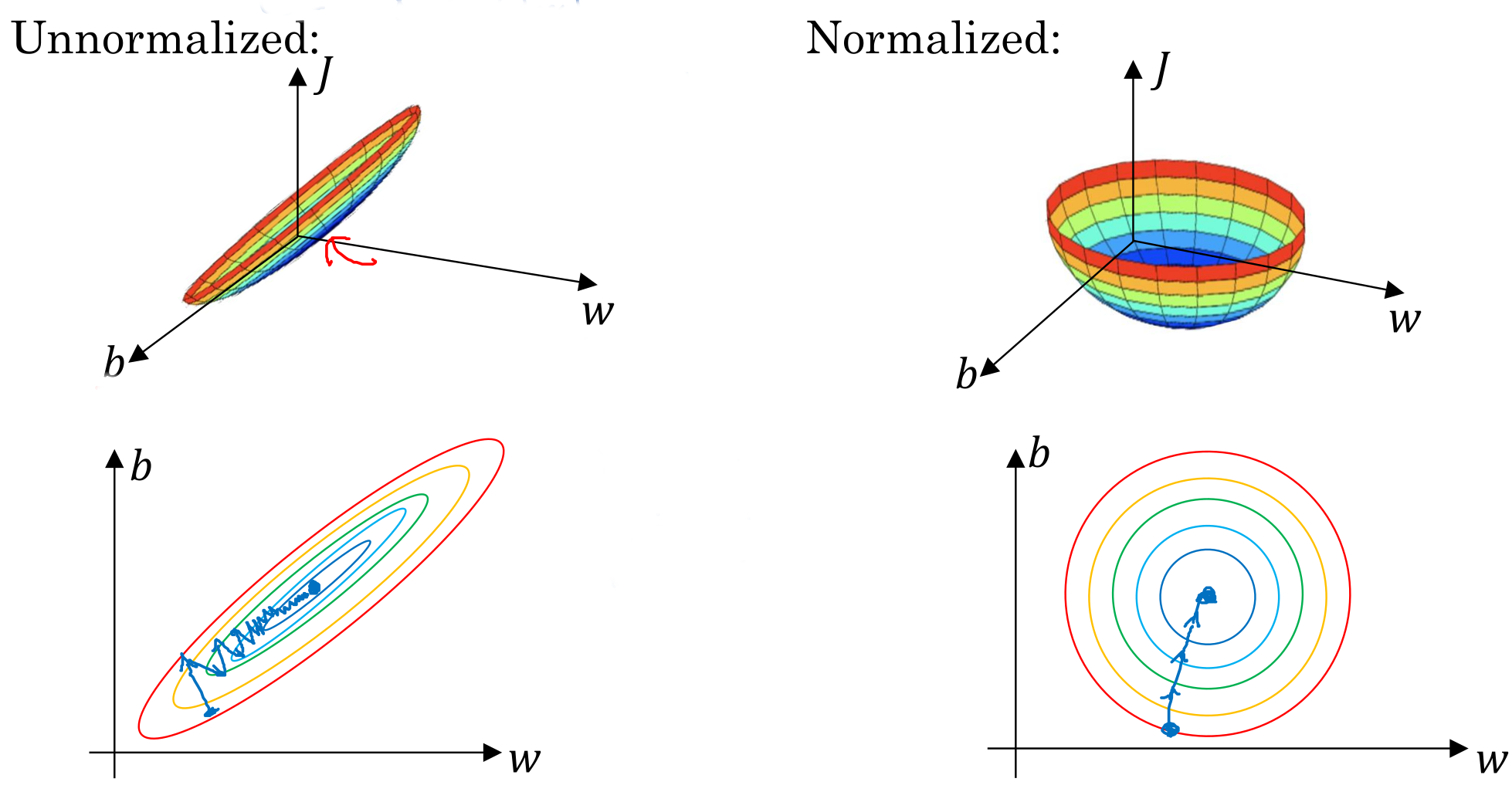
除了对GD的优化外，我们也可以对数据进行规范化(Normalize)，来加速训练过程。一般采用的方式是计算样本数据各纬度的均值和平方差，而后计算得到新的、规范化好的样本数据：

在规范化完成以后，我们可以看到，整个样本空间的形状会更加”优雅”，这种良好的状态，可以让梯度下降法更准确的”瞄准”最优化目标，也可以降低数值计算误差，进而加快训练的收敛。

如何进行DNN的训练优化，这几年是一个很热门的领域，依旧有不少学者在数值计算、算法、计算引擎及硬件方面进行着各种的研究。这里的一些调整，只是一些最常见、最粗浅的部分，感兴趣的可以进一步调研、深入了解。