今天记录的论文为: 《Dominant Resource Fairness: Fair Allocation of Multiple Resource Types》(nsdi’11)。这篇论文介绍了在多资源纬度场景下（比如CPU和Memory）的调度算法，证明了算法所具备的几个重要的特性。写这篇博文的时候，只看了其中的前几节，摸清楚整个算法的大致思路，后面的数学证明还没看。因此这篇博文严格说只是半篇介绍，作为后面介绍的一个引子。

废话不多说，先直接用论文中的一个简单的例子来说明算法思路:

考虑一个有{9 CPUs, 18GB RAM}的资源池。有两个User A和B，向这个资源池申请资源执行自己众多的Task。出于简化问题的考虑，我们认为一个User下的所有Task的资源需求都是同质的。比如在这个例子中，A的每个Task需要的资源为{1CPUs, 4GB}，B需要的是{3CPUs, 1GB}。那么如何分配资源池的资源给User A和User B才算合理呢?

论文的算法认为max-min fairness是合理的，即最大化最小资源分配者的资源总量(maximizes the minimum allocation received by a user)。简单的说，如果系统发现一个用户当前分配到的资源在总池子中的占比(share)较少，那么就应该优先将资源分配给这个倒霉的用户。换句话说，如果用户任务数都是足够的，那么对于有n个用户的系统，理论上用户得到的资源应该都是池子的\(\frac{1}{n}\)。这个优化目标在单一纬度的资源模型上是没有问题的。比如只有CPU，我可以把资源给当前CPU分配量最少的那个用户。但在对多纬度资源的场景下，比如这个case中需要同时考虑CPU和Memory，又应当如何处理呢？

文章提出的基本思路是『看主导的那一维资源』(Dominant Resource)就可以了。什么意思呢？比如上面这个case，对于用户A来说，其cpu需求对池子的总CPU资源占比(share)为\(\frac{1}{9}\)，而memory为\(\frac{4}{18}=\frac{2}{9}\)，因此其Dominant Resource share就是memory的那个\(\frac{2}{9}\)，而B则为memory那个纬度的\(\frac{1}{3}\)。整个算法的优化目标就是让所有用户的Dominant Resource share值尽可能的”相等”。比如在上面的例子中，假定在池子中启动了\(x\)个User A的Task和\(y\)个User B的Task，那么问题就表达为:

• \(x + 3y \le 9\) && \(4x + y \le 18\): 即各纬度总分配量受限于资源池总量;
• \(\frac{2x}{9}=\frac{y}{3}\): Dominant Resource在池子中的占比尽可能相等, 即Dominant Resource Fairness的含义

由上面的方程可以解得{x=3, y=2}, 即启动3个A用户的Task，2个B用户的Task。二者分配的资源为A:{3CPUs, 12GB}, B:{6CPUs, 2GB}。

在工程实现中，上面的思路可以翻译成如下算法:

这个算法的思路很简单，即维持记录当前用户的Dominant Resource的share值的大小，每次从中挑选最小的那个，只要资源足够就把这个用户的任务启动起来。

在这个算法下，上述问题的执行过程为:

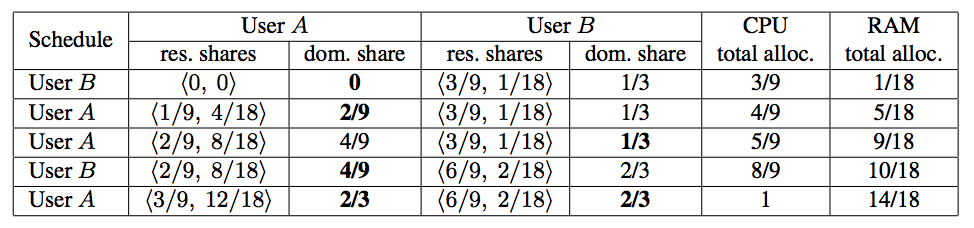
• 刚开始的时候，假如先启动了B的一个任务，那么此时的Dom.share值为: \(\to\{A:0, B:\frac{1}{3}\}\)
• 因为A比较小，启动A的下一个任务。\(\to\{A:\frac{2}{9}, B:\frac{1}{3}\}\)
• 然后还是A比较小，继续启动A的下一个任务。\(\to\{A:\frac{4}{9}, B:\frac{1}{3}\}\)
• 接着B比较小，启动B。\(\to\{A:\frac{4}{9}, B:\frac{2}{3}\}\)
• 然后A比较小，启动A。\(\to\{A:\frac{2}{3}, B:\frac{2}{3}\}\)

此时，由于CPU资源已经被分配完了，因此算法结束。上述过程出于简单考虑，没有处理任务结束的场景。在实际实现中，任务结束的时候，也需要更新具体的Dom.share值。此外，可以对每个用户增加一个”权重值”，对share执行修正，以适应不同用户资源分配量不同的场景。不论哪个变种，算法的基本思路不会发生变化。

至此算法的基本思路介绍完毕，下一篇blog会讲解这个算法具备的特性，并进行数学上的证明，敬请期待。