在DRF论文中，将DRF与以下两个调度算法进行了比较：

• Asset Fairness: 这个调度算法的基本思路是，让所有的user的各资源的share之和最小，即对\(x_{i} = \sum_{j} s_{i,j}\)(\(s_{i,j}\)表示用户\(u_{i}\)在资源\(R_{j}\)上分配到的资源)的加权结果执行max-min fairness算法。这个算法背后的假定是: 对于不同纬度的资源，其share值是等价的，即1%的CPU和1%的内存，其价值是相等的。
• CEEI(Competitive Equilibrium from Equal Incomes): CEEI算法的思想来自于微观经济学，其基本思路: 假定所有user初始都占有资源的\(\frac{1}{n}\)，然后允许用户在一个完全竞争的环境下交易自己多出来的资源。这个解就是Nash bargaining solution。Nash bargaining solution解为使得\(\prod_{i} u_{i}(\alpha_{i})\)最大的解，其中\(u_{i}(\alpha_{i})\)表示用户\(u_{i}\)能够从他的分配中获得的最大”利润”。在这个场景中，\(u_{i}(\alpha_{i})\)其实就是\(s_{i}\)(瓶颈资源限制了能够启动的task数目)，也即CEEI的解为使\(\prod_{i} s_{i}\)最大化的分配结果。

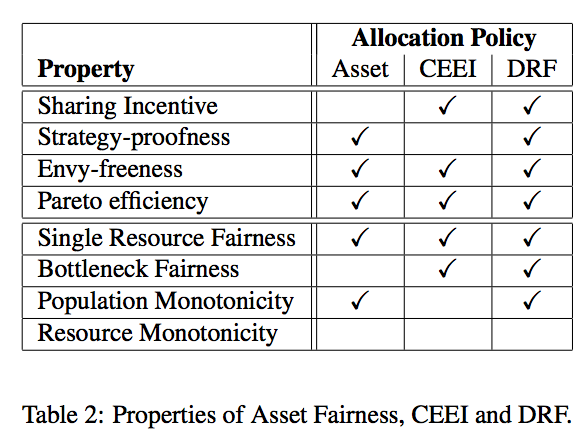
从上面的论文截图可以看到，Asset Fairness、CEEI和DRF具备的相比，他们的差异关键在以下两点:

• Asset Fairness不具备Sharing Incentive属性，即采用Asset Fairness调度算法的，用户会倾向于独占资源池而不愿意和其他用户合并池子、共享整体资源。
• CEEI不具备Strategy proofness属性，即用户有办法通过虚报资源需求，来让自己获益。

显然，这两个属性的缺失，在大规模部署、面向用户众多的场景下，都是很有问题的。论文选择这两个算法其实感觉还是很有讲究的。说实话，在读这篇论文之前，尽管不知道Asset Fairness和CEEI算法，我也凭直觉构造出几乎一致的调度算法，而且自以为效果应该会不错。但读过这篇论文后，猛然惊醒，假若将这些算法真的应用到线上，长久运行之后对整个资源池子的管理就会出现很大的问题。DRF这篇论文，告诫我们: 调度算法不能靠直觉、而应当有比较精细的理论论证，或者至少有一定的实验评估¹。我们需要扭转自己的思维方式。我愿意花很大的精力去细读、并详细写出这几篇blog的原因也在于此。

附: Asset Fairness和CEEI不满足的属性²

Theorem-10: Asset Fairness不满足Sharing incentive属性。

证: 假定总资源为<30, 30>，两个用户的资源需求为\(D_{1}\):<1,3>，\(D_{2}\):<1,1>。那么按照AF的算法: \(x_{1}=\frac{1}{30}+\frac{3}{30}=\frac{4}{30}\)，\(x_{2}=\frac{1}{30}+\frac{1}{30}=\frac{2}{30}\)，于是第一个\(u_{1}\)启动6个、\(u_{2}\)启动12个任务(因为\(6 x_{1}=12 x_{2}\))。也即\(u_{1}\)拿到了<6, 18>、\(u_{2}\)拿到了<12,12>的资源，\(u_{2}\)拿到的资源还不到池子总资源的一半，因此\(u_{2}\)会倾向于独占总资源的\(\frac{1}{2}\)(<15, 15>)以启动更多的任务(可以起15个)，违背了Sharing-incentive。\(\Box\)

Theorem-14: CEEI不满足strategy-proof属性。

证: 假定总资源为<100, 100>，两个用户的资源需求为\(D_{1}\):<16,1>，\(D_{2}\):<1,2>。那么CEEI的分配结果\(u_{1}\)启动\(\frac{100}{31} \approx 3.2\)，\(u_{2}\)启动\(\frac{1500}{31} \approx 48.8\)的任务。如果用户将自己的资源需求虚报为<16,8>，那么CEEI的计算结果为\(u_{1}\)启动\(\frac{25}{6} \approx 4.2\)、\(u_{2}\)启动\(\frac{100}{3} \approx 33.3\)。\(u_{1}\)通过欺骗手段多启动了任务(\(3.2 \to 4.2\))，损害了\(u_{2}\)的利益(\(48.8 \to 33.3\))，因此CEEI不满足strategy-proof属性。\(\Box\)