前面一篇对queue-based的经典策略做了一个概要性的介绍。整体来说，queue-based的调度算法是一种”启发式”的算法，这类算法一般给人一种”拼凑”感，有一定道理但又让人有些”放心不下”，深怕在啥地方存在什么漏洞。Quincy这篇论文则提出了一个全新的建模工具，将调度问题转变成了一个Flow-based的最优化问题，并用此工具给出了基于数据局部性的一个最优化调度策略，让人耳目一新。

Quincy将调度问题表达成基于下图的一个最优化问题(min-cost network flow):

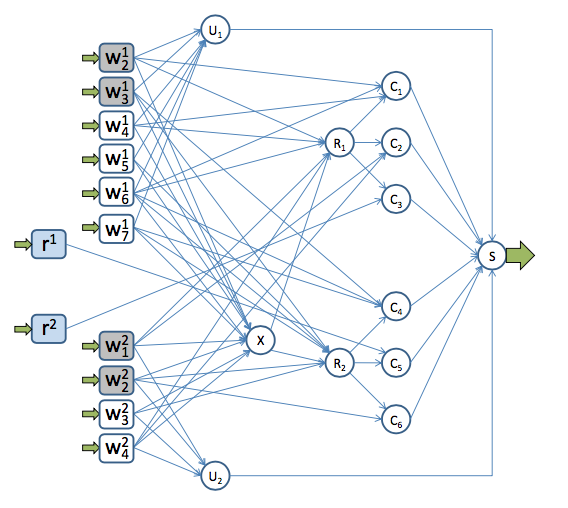
整个图的含义是，图上有一些货物，包括计算作业的root-task(\(r^{i}\))、worker-task(\(w^i_{j}\))，需要通过图中的一系列节点和边”运送”到”目的地”\(s\)。这些货物通过边的时候，需要付出一定的”代价”(cost)，并且通过边的货物总量是有”容量”限制的(capacity)。如何用最少的cost将”货物”运送到\(s\)？对这个图的求解，就是基于当前信息调度器可获得的一个”最优”解。

图中的\(c_i\)节点表示一台机器，\(u_i\)节点表示job-i的pending队列。我们可以观察发现一个task(\(r^i\)和\(w^i_j\))，有且必然通过某个\(c_i\)或者\(u_i\)节点。如果图的求解结果中，\(w^i_j\)通过了\(c_h\)，那么就意味着\(w^i_j\)被调度到了机器\(h\)上；同样如果\(w^i_j\)指向了\(u_i\)，则意味着\(w^i_j\)被塞进了pending队列等待下一次调度。

剩下的问题就是，如何构造合适的中间结点和边(如何连接、cost/capacity怎么计算)，来表达出算法的优化目标。在Quincy这篇论文里，其核心优化目标为：尽量将作业调度到数据所在的位置、以减少计算数据的传输量，提高整体吞吐。

为表达作业放置偏好，作者引入了两类特殊的中间结点：

• \(R_r\): 表示一个机架(Rack)，入边与task相连，出边连接着这个机架上的机器(如上图中：\(c_1\)、\(c_2\)、\(c_3\)在\(R_1\)上)。如果一个\(w^i_j\)(或\(X\))连入，表示这个任务可以调度到对应机架下的任意一台机器上。
• \(X\)：表示一个Cluster，与\(R_r\)非常类似，入边连接任务、出边连接这个Cluster里面的\(R_r\)，表示任务可以调度到这个Cluster的任意一个机器上(流过\(R_r\)节点)。

每一个job到达的时候，都会由root-task计算得到prefer-computer和prefer-rack列表，比如\(w^1_6\)的prefer-computer为[\(c_1\)、\(c_4\)]，prefer-rack为[\(R_1\)、\(R_2\)]，那么就会在\(w^1_6\)和\(c_1\)、\(c_4\)、\(R_1\)、\(R_2\)间建边。如果一个task已经正在某台机器上运行，则在这个task和所在机器建边，如上途中\(w^1_2\)在\(c_1\)运行，则\(w^1_2\)和\(c_1\)间有一条边，且cost为0。

那么如何设置边上的权重呢？其实只要想清楚这些节点的含义，这个cost并不难构造。基本来说，有以下几个考量：(a) 如果把\(w^i_j\)调度到\(R_r\)或者\(c_h\)下，需要传输的字节数; (b) 如果运行中的任务被抢占，需要付出的惩罚代价。这个代价一般和该任务已经运行的时间或者计算进度有关; (c) 如果一个任务被放进pending队列，所需要付出的惩罚代价。一般这个代价和该任务的等待时间有关。

不同的单位之间(比如上面传输的字节数、和等待时间)，可能需要定义一个归一化的方式将不同的纬度揉和起来评估。比如，\(w^1_2\)在\(c_1\)上运行，那么边\(cost(w^1_2 \to c_1) = 0\)，如果我将\(w^1_2\) kill掉重新放到pending队列需要付出的惩罚代价定义为：已经完成计算的数据量+任务已经提交的时间，那么我就可以定义\(cost(w^1_2 \to u_1) = \lambda ExecutedBytes + \rho (CurrentTime - SubmittedTime)\)，诸如此类。这个权重的计算非常直观。在Quincy论文后面的附录部分，详细给出了Quincy推荐的权重计算的方式，这里不再一一赘述，感兴趣的可以自行阅读或者尝试设计，这里不再赘述。